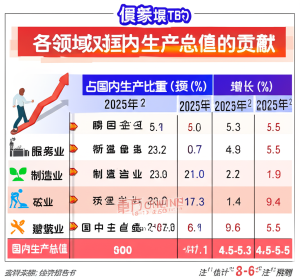
牛顿法的历史与现状
牛顿法是一种经典的优化算法,其历史可以追溯到三百多年前。牛顿法的核心思想是通过泰勒展开式近似函数,从而找到函数的极值点。这种方法在数学和工程领域中有着广泛的应用,尤其是在求解非线性方程和优化问题时。牛顿法的收敛速度快,通常在几次迭代后就能接近最优解,因此在实际应用中非常受欢迎。
然而,传统的牛顿法也有其局限性。首先,牛顿法需要计算函数的二阶导数,这在某些情况下是非常困难的。其次,牛顿法对初始值的选择非常敏感,如果初始值选择不当,可能会导致算法收敛速度变慢甚至收敛失败。此外,牛顿法在处理大规模问题时,计算成本较高,这限制了其在某些复杂问题中的应用。
三位数学家的创新
近期,三位数学家对牛顿法进行了改进,使得这个算法在收敛速度和函数范围等方面都有了显著提升。改进后的牛顿法不仅保留了传统牛顿法的优点,还克服了其部分局限性。具体来说,改进后的牛顿法在以下几个方面进行了优化:
实际应用中的突破
改进后的牛顿法不仅在理论上有了突破,在实际应用中也产生了巨大的影响。在优化问题中,选择合适的算法对于解决问题至关重要。传统的牛顿法虽然效果显著,但在某些情况下也存在一定的局限性。而这次改进后的牛顿法,为解决更加复杂的优化问题提供了新的可能性。
例如,在机器学习和人工智能领域,优化算法是训练模型的核心。改进后的牛顿法可以显著提高模型的训练速度和准确性,从而推动人工智能技术的发展。此外,在金融、物流和制造等领域,优化问题也非常普遍,改进后的牛顿法可以为这些领域提供更高效的解决方案。
数学研究的不断进步
对牛顿法的改进也反映了数学研究的不断进步和创新。数学作为一门基础学科,一直在不断发展和变化,为其他领域的发展提供了坚实的基础。数学家们的努力与创新,推动着数学领域的发展,也为科学技术的进步注入了新的活力。
数学研究不仅仅是为数学本身服务,更是为解决实际问题提供了理论支持。改进后的牛顿法就是一个典型的例子,它不仅在数学领域有了突破,也为其他科学技术领域带来了新的思路和方法。
未来展望
综上所述,三位数学家改写经典牛顿法,使得这一经典算法焕发出新的活力。这一突破不仅仅是数学领域的创新,更是对整个科学技术领域的贡献。期待这一改进后的牛顿法能够为更多领域的问题提供解决方案,推动科学技术的不断进步。
未来,随着数学研究的不断深入和技术的不断进步,我们有理由相信,牛顿法及其他优化算法将会在更多领域发挥重要作用。数学家们的创新精神和不断探索的态度,将为科学技术的发展注入新的活力,推动人类社会的进步。
总结
牛顿法作为经典的优化算法,其改进不仅在数学领域有了突破,也为其他科学技术领域带来了新的思路和方法。三位数学家的创新,使得牛顿法在收敛速度和函数范围等方面都有了显著提升,为解决更加复杂的优化问题提供了新的可能性。未来,随着数学研究的不断深入和技术的不断进步,牛顿法及其他优化算法将会在更多领域发挥重要作用,推动科学技术的不断进步。